PART 2
In the last issue we published an article entitled “Is the Universe Large Or Small?” in which we critiqued the claims of Harald Heinze of Switzerland. At the time we offered Mr. Heinze up to 30 pages to respond. In this issue Mr. Heinze responds and I will reproduce his response without inserting any of my comments. My response will follow after. In the following, passages from the last issue, referred to by Mr. Heinze, are in italics.
I refer to the page numbers in issue number 73:
Pp. 12-13: Unfortunately, nothing I've read by Alfven suggests a new physics of the type required. Indeed, I've seen nothing which suggests that Alfven believes in anything but a large universe. If Mr. Heinze wants to pursue this point he must at least give complete references into the literature or, best of all, be willing to send (or loan) copies of the articles to his critics.You complain that I do not give proper references, but neither do you. Aspden and especially Th. van Flanderen are cited only, as I did with Alfven. You base your model on your firmament concept derived partly from Aspden's ideas. Okay, that you can do. But that is no proof that Aspden's model is correct. He has opponents, as you know and the whole concept of an “ether” is vague and meets many problems. (See, for instance, the literature on the interpretation of the Michelson- Morley experiments). I do not definitely say that an “ether” cannot exist, but it is only one model among many. So your concept is based on a hypothesis of Aspden.
Further: you arbitrarily fix the space my model has to be located among three possibilities. My model is not based on a “miracle” but on physics. To take away misunderstandings concerning my position, about which you are unclear: I tend to think that geocentricity comes much closer to reality than the heliocentric point of view. However, I am not (yet) decided about the final details of geocentricity. I know that you interpret geocentrism as absolute, i.e. no rotation or orbit of the earth. What concerns the daily rotation of the earth I am not (yet) decided. I do not yet have clear understanding what is meant in the Bible about the fixed position of the earth. (Fixed with respect to what?
P. 14: Unfortunately, nothing I've read by Alfven suggests a new physics of the type required. Indeed, I've seen nothing which suggests that Alfven believes in anything but a large universe.You have seen nothing in Alfven's writings that would suggest a small universe. But likewise I have seen nothing in Aspden's writings that would suggest a geocentric universe. So why do you blame me for taking idea from Alfven? But, Alfven's plasma physics does support a concept of a small universe. For instance, in his article “Model of the Plasma Universe,” I.E.E.E. Transactions of Plasma Science, vol. PS-14, no. 6, December 1986, p. 629 ff. On page 633 he writes about star formation (and so naturally resulting star sizes): “As stated above, the general believe [sic] that electromagnetic forces oppose the contraction of a cloud is not necessarily correct. Pinch effects may contribute to the concentration and, indeed, cause a collapse of clouds with a mass that is orders of magnitude smaller than the Jeans mass.” (Emphasis mine.) Similar arguments and expansions are made by Halton Arp in his article” Gas, Dust and Plasma in Extragalactic Space,” Laser and Particle Beams, vol. 6, part 3, pp. 39-403, 1988. Arp wrote, for instance: “There may be large errors in the currently assumed distance scales in the universe.” (I.e., much smaller.)
Pp. 15-16: The point of that paper is that both the ballistic theory and the wave theory can account for Michelson's observation. Michelson had erroneously claimed that his observation disproved the ballistic theory. Since both theories can account for the observation, if this is the aforementioned “irrefutable evidence,” mentioned by Harald, then he has totally deluded himself here in presenting this as a “proof” for the ballistic theory. An observation explainable by two competing theories cannot be held as proof of one over the other.The turning of the mirror, overlooked by Michelson in his experiments with star light (Astrophysical Journal, p. 190 ff., 1913,) has only one explanation left: the “tennis- racket” principle of light propagation: the light reflected by moving mirrors we get double the speed of the mirror itself added. This experimental fact is in agreement with the calculation of this experiment taking into account the turn of the mirror and so with the ballistic theory of light only, not with the ether-wave theory. However, this fact does not exclude that light can be a “bundle” of photons which behave like a wave.
Not only that, it is known since about 100 years ago, since the investigations of Poynting, Lorentz and Poincaire, that light has impulse [momentum - Ed.], and so also mass. The fact that relativity claims that light has zero rest mass is nothing but a definition in the relativity equations and has no physical experience behind it. The experiment described below does prove that light has mass, because it gets the double reflection velocity from turning mirrors. Only from these facts, the ballistic theory gets crucial support, and so support also for much smaller distances in the universe, as will be seen below.
Michelson proves the ballistic theory of light
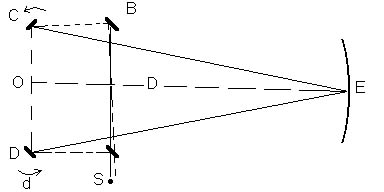
Figure 1 is taken from the aforementioned Astrophysical Journal reference by Michelson on page 190.
In figure 1, light from a source S falls on the weakly-silvered mirror, A. A reflected part of the beam runs to the orbiting mirror D, then to the concave mirror C (orbiting also around the axis O, as does mirror D), and then to the mirror B, which throws the beam back to A. The part of the beam which passed runs the opposite way back and returns via DA to the starting point, where it meets the first beam described and produced interference fringes. According to the wave theory (supported by Gerardus) the velocity of the light beam is independent of the velocity of the orbiting mirrors, while the ballistic light theory, (which I support) requires that the velocity of light depend on the mirrors involved.
According to the theory of elastic rebound r=2, should the mirror act like a new source then r = 1. The light tracing the part DEC requires a running time, T1 = 2(D+d)/V1 and the path CED takes T2 = 2(D-d)/V2, where D is the distance OE, d is the distance by which the mirror traveled while the light beam ran through DEC. V1 is the velocity of the first beam and V2 that of the second, opposing beam.
So the running time difference is:
where v is the velocity component of the mirror in the direction of the
reflected beam. [At this point I, as editor, must interject that in what follows
the subscripts have been dropped off the V terms and there is no
way to reconstruct which is which since only one remains. From this
point on the assumption that the speed of the mirror adds or subtracts
from the speed of light has been removed and the wave theory, not the
ballistic theory is being presented.] Now d/2D = v/V, from which we
conclude that T1-T2 = 4 (2-r)(D/V)(v/V). The corresponding shift for the
interference fringe is D=V(T1-T2)/l=4D(2-r)(v/V)/l where l is the
wavelength. For r=0 then, D=8Dv/(Vl); for r=1, D=4Dv/(Vl); and for
r=2, D=0.
Then Michelson goes on to derive the formula for the fringe shifts.
Michelson observed 3.77 interference fringes per 1,000 r.p.m. He derives
a weighted average of 3.81 and a computed shift of 3.76 fringes for his
apparatus. Michelson writes: “You see, that within the error limits of observation
(perhaps 2%) the velocity of a moving mirror has no influence
on the velocity of the light reflected at its surface.” (Translated by H.
Heinze).
Now to show where Michelson erred. Michelson wrongly calculated
the path of the light. He takes the total distance to be 2(D+d) because d is
traversed both on the way out and on return from and to the returning
mirror respectively. But the impact of the returning mirror itself has to be
taken into account! We look at the first beam, which comes from E and
falls on slightly to the left turned mirror C (turned by the amount d or by
angle d/R). The beam CB will consequently be turned up by 2d/R
(symmetric reflection). It results that (to begin with) the distance CB is
slightly shortened, but this shortening is compensated by the opposing
beam EDA and so is to be ignored in the final calculation. Further, because
the reflected beam from B to A is returned by 2d/R, which, because
of the 45-degree angle of mirror A results in shortening of the distance of
2R, 2d/R = 4d. At the opposing beam this path drops out also and so
does the shortening associated with it. Because 4d = 8Dv/V, the running
time difference is accordingly increased and must correctly be written as
T1-T2 = 4(D/V)(4-r)(v/V).
For the interference fringes, the new formula is D=4D(4-r)v/(Vl).
For r=0, D=16Dv/(Vl) which is predicted by relativity and ‘ther theory,
for r=1, D=12Dv/(Vl) which is re-emission theory, and for r=2,
D=8Dv/(Vl) which is what Michelson observed and which matches the
ballistic theory of light. Only the last theory, the ballistic one, is in accordance
with the experiment! A)If my small universe is being upheld, then naturally the diameters
and velocities concerning the binary star systems must be much smaller
than the 30 km/sec proposed by Gerardus. If the center star is comparable
with planets in size, then naturally it cannot have companions at
about 150 million kilometers distance (as, f.i., in our solar system the
earth-sun distance requires the earth to orbit at 30 km/sec.)
B) And this is very important and overlooked by Gerardus: the calculation
of binary star orbits (both velocities and orbit diameters) is based
on circular reasoning: that calculation supposes an unambiguous
knowledge of star motions. The only direct knowledge of stellar motion
is provided by the light received from the stars. It is therefore circularly
unproductive to infer the speed of propagation of the light emitted from
moving stars on the basis of the motion of stars, since the only direct
knowledge of the stellar motion is provided by the very same light whose
speed of propagation will have its effect in the observed motion of stars.
Thus the appearance of ghost-stars and distorted orbits could not be
recognized a such, unless the speed of propagation of the light were
known independently beforehand.
C) The exact indirect inference of binary stellar motion from celestial
mechanics is also circular, since all celestial motions are only known
(those outside the solar system) exactly by the light or other radiation
received from the celestial bodies.
So all of Gerardus' arguments in this respect are under these
reservations!! Nevertheless, if the ballistic theory of light propagation is
correct (and the above experiment, famous and accepted throughout the
whole scientific world but mistakenly interpreted as shown above) proves
that beyond the shadow of doubt, then the velocities , orbits, etc. of binary
stars must be considerably smaller than calculated so far in the
literature! That also means that all distances are smaller by a comparable
amount.
D) An additional fact is overlooked: while all visible binaries have
small velocities and are believed to be nearby (because all components
can be separated in the telescopes), the binaries's spectra are absorption
spectra, where the velocities measured are those of the absorber to the
observer, not of the binary star components!
E) According to an investigation, now already about 35 years ago by
Prendergast (astrophys. Journal, 1960, p. 162), all components of a close
binary system are embedded in a single atmosphere! I enclose a sketch
from Prendergast of the orbit models involved (Figure 4). There it is to
be seen that the outer velocities are much bigger than the real velocities
of the stars! Also, the visible companion often times is the bigger one,
the smaller one, the one with the bigger orbit, which mainly determines
the outer velocities of the binary system!
If you further realize how difficult it is to construct orbits of binary
stars (see, for instance, W. H. van den Bos, “Orbit Determinations of
Visual Binaries” in Stars and Stellar Systems vol. 2, 1962 U. of Chicago
Press, p. 556 where he reports confusion of orbit calculation between orbits
of 20 and 240 years!) and, if you further know that the ballistic
theory drastically shortens orbit velocities, orbit diameters and distances,
then your arguments concerning line distortions and ghost spectra become
completely invalid. The more because in the small universe distances,
star sizes and orbit diameters are much smaller!
About the claim of double or triple appearances and/or occultation
with respect to the ballistic theory the arguments of Gerardus have been
refuted since long: in 1939 by Oskar Mathias in Physikalische Zeitschift,
pp. 443-460: “Die ballistischen Lichttheorien und das Prinzip der
Konstanz der Lichtgeschwindigkeit,” wherein Mathias refutes the claims
of deSitter (arguments those of Gerardus). Then by Rudolf Nedved in the
Toth-Maatian Review, vol. 6, no. 4, Jan. 1988, pp. 3355-9, “The Light of
Binary Stars.” In the summary of the last article mentioned, the author
writes about the ballistic theory of light: “The consequent analysis of the
propagation of light from double stars shows, that the overtaking of
beams of different speeds occurs only in nodes located sporadically in
space at enormous distances. the packets of light from different parts of
orbit pass these nodes at light velocity, thus for each observer only as a
mere flash. The probability of finding the doubling of spectra lines
equals thus practically zero. Thereby deSitter's objection against the dependence
of light velocity on the motion of source falls as entirely
baseless.” So Gerardus is wrong if he tries to capitalize on this point because I
did not at all deny star movements seen in the Magellanic Clouds but I
denied only the validity of the procedure how they were measured.
P. 24: Gerardus's figure 3 [reproduced as Figure 2, here] is simply
wrong in describing parallax measurements with very long baseline interferometry.
He depicts the star as a point and the earth with a big circle,
so connecting them with a triangle. But I wrote and Gerardus referred to
it in his article, that the star have sizes comparable to planets. So the
lines connecting earth and star should either go out parallel or in small
angles expanding or contracting to fit the star (Figure 3).
P. 16: The problem with the ballistic theory in a small universe is that
in close-binary star systems, with orbital periods of a few hours, one expects
to see multiple images of the stars in their orbits. (For a large
universe the problem expands to include stars with periods of months or
even years.
Now Gerardus criticizes the ballistic theory pointing to inconsistencies
to be observed in binary stars if the theory is correct. I
want to answer the following:
P. 20: But even if a photon could be stretched out in the way Harald
suggests, in half the cases, the tail of the photon would catch up with the
head, pass it, and reach the earth before the head. In the other half, the
photon would stretch itself longer and longer. This means that there is a
time when the photon is of length zero and has an infinite energy density.
Even at the temperatures in a light bulb, this catch-up time is only 1,000
seconds. From the surface of the sun it's about 300 seconds, but 8
minutes, the time it takes light from the sun to travel to earth, is 480
seconds.
Gerardus comments on the beginning and end of a single wave
train within the ballistic picture. This matter is already treated above.
Also, “photons” do not come in single “bullets,” but in bundles. But this
is not important. Even if the single photons would have no connections
at all, the result would not differ! Therefore also Gerardus' reference to
the sun is senseless.
P. 21: The huge distances I “support” are not at all based on redshift.
They're based on the experimentally determined values for the gravitational
constant (which relates mass, force and distance), the speed of
light (which relates the permeability and permitivity of space), Planck's
constant (which relates energy and light), the amount of charge of an
electron or proton, and, finally, Boltzmann's constant (which relates
energy to temperature.)
The permeability and permittivity as well as
Planck's constant Gerardus refers to with respect to his understanding of
”the huge distances” would cover many pages. I have evidence that none
of them has any real physical meaning, but are simply mathematical gaps
which stand for non-understanding of Maxwell's inventions of these two
concepts. What concerns Planck's constant, such a constant is non-
existent in nature. It is based on Boltzmann's confusion of the discrete
velocity space of his model with a continuum. Later Planck, Heisenberg
and Schrodinger (to a lesser degree) have overtaken this confusion and
constructed the constant. This “constant” is composed and a variable.
P. 21, part 2: Actually, the “speed values” of the rim [of the Coma
cluster of galaxies] were much lower than those a third of the way out
from the center.
On the same page Gerardus claims that the speed values
at the rim of the Coma cluster are much smaller than supposed by me.
But this makes his big universe even more realistic. If these “small” rotation
speeds are being upheld, the age of the universe would be many
hundreds of billions of years. If the Coma cluster would be really as big
and distant as Gerardus claims, because the rotation structure of this
cluster shows several turns. In my small universe the small velocities are
to be expected and nicely fit Biblical age as well as small distance and
size of the Coma cluster.
P. 21-22: I doubt that Hubble refuted van Maanen's claims that there
is star motion seen within galaxies such as the Andromeda galaxy. I have
seen Hubble's arguments but Hubble's ideas and the experimental
material he presented in the thirties is based on preconceived models of
reference frames for galaxies.
If the earth is in the center of the universe,
then galaxies most probably would rotate around the earth, and so change
”proper motion” values. Only here Hubble did not know the real picture.
And because he did not accept the universe to be structured with respect
to the center, the earth, this mistake influenced his refutation of van
Maanen who himself was a highly respected investigator and experimenter
in astronomy, more so than Hubble who only later became
more famous for his expanding universe.
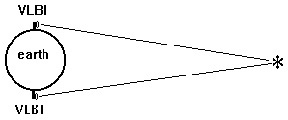
Figure 2: Absolute parallax measurement using Very Long Baseline Interferometry.

Figure 3: Heinze's interpretation of VLBI.
The reader can readily see that in Heinze's interpretation the parallax is the diameter of the star. Elsewhere, Heinze vehemently protested that VLBI CANNOT measure the diameters of stars.
There is more to say about Gerardus' claim that VLBI should show a parallax if stars are as close as I think. I have recalculated this claim and came up to the result that the parallax angle resulting from VLBI measurements in this matter would be about 400 to 500 times smaller than that measured for the star Proxima Centauri claimed to be about 4.3 light years away. That would mean that with VLBI the parallax of a star could be measured which is about 2,000 light years away. You can forget such claims. Further, Gerardus's claim is complicated by his wrong figure 3 and the fact that light does perhaps not run in a perfect straight line over these alleged huge distances (what must be known for the claims of VLBI measurements). It is, however, already known that light can deviate from a straight line by about 1.75 arc-seconds even within the small earth-sun distance (bending of starlight passing through the sun). Everywhere in space there are electromagnetic fields, stars, galaxies, dust clouds, etc. affecting the light path. So such a high precision is, in my eyes, an illusion.
Page 25: Evidence for the current “spectral analysis” includes not only the sun's surface but any spectroscopy lab anywhere in earth.Gerardus claims, concerning star spectra, that we already know most of that subject and only minor progress or corrections are done in the past or are to be done in the future. Nothing is more wrong than that. I give you here only three references from my files (out of many others) which refute Gerardus' statements:
a)D. Mihalis, 1978. “Model Atmospheres,” in Stellar Atmospheres,” (San Francisco: W. H. Freeman), 1978.
b) G. Worrall and A. M. Wilson, 1972. “Can Astrophysical Abundances be Taken Seriously?” Nature 236:15-18.
c) “The Future of Stellar Spectroscopy and its Dependence on You,” 1991. Physica Scripta T34:14-19.
In these articles and naturally also in those of Alfven and others, the fundamentals of stellar spectroscopy are critically commented on.
Page 26: Yes, stars can be as small as I proposed (see Alfven's remarks on star formation above). If clouds which form stars can be ”orders of magnitude smaller than the Jeans limit,” the star cannot be bigger than the material it is formed from! Now it is up to Gerardus to show that the stars of planetary size cannot show spectra as seen today in nature!
Page 27: About star diameters, Harald wrote in Biblical Astronomer no. 73 that: “And I do not know the individual diameters and many other parameters of the small stars.” To which I responded, “Why not, they've been published in magazines like 'Sky and Telescope'.”
Again star diameters. No, the star diameters shown in Sky and Telescope etc. are definitely not measured diameters but simply angle measurements “equipped” with a big distance. Further, gravitation can power a star, but the contraction has not been observed. But my star model, where power is generated by rotation, this rotation is seen at all stars and is experimental fact. The fact that statistically, faster rotating stars are hotter, speaks for my hypothesis.Varshni's hypothesis that quasars are stars is confirmed by the Hubble telescope observation, not refuted! However, Gerardus fails to distinguish between the many different quasar types.
Page 28: Gerardus should continue to pursue his investigation of small stars. They do not “fly apart catastrophically.” The “magnetic bottling” parameters are real, but most probably much different from Gerardus' understanding of them because, as he confesses, he did not read much of Alfven's work and did not find his work on small stars, although it is there (see above references).
Finally, I now come to the hard “facts” supporting the small universe which Gerardus asked me for a long time ago. Besides the above arguments I will here show only two examples which have appeared in the international press and which were partly also tackled by Gerardus in his last issues of the Biblical Astronomer. I mean the famous, spectacular supernova of 1987 in the Large Magellanic Cloud, i.e., SN 1987A. Hereunder is my criticism and positive evidence for a small universe, based on this supernova investigation. The other subject is Cepheid variables as distance indicators in space.
Supernova 1987A
1)Gerardus tried to give evidence in several of the recent bulletins that the investigation of this supernova would have resulted in confirmation of the claimed 170,000 light-years distance of the Large Magellanic Clouds. Gerardus gave an example of a calculation based on light travel times between the supernova, a surrounding light/dust ring and earth. He came out with an interesting “confirmation” of the claimed distance. However, he did not mention that there is not just one ring involved but at least three at different distances from the supernova. Moreover, an expert who is directly involved in this research (L. Wang, European Southern Observatory, Garching, Munich, Germany) wrote me that such calculations are in no way justified. (Private communication, Dr. L. Wang, dd. February 11, 1992.)I have a nice color picture of those ring structures surrounding the supernova and I suggest that Gerardus place it on the front page of the next Biblical Astronomer.
2)The ring structure around the supernova SN 1987A is claimed to expand with a velocity of 20 to 40 times the speed of light, if measured by angular methods. Why this? Because it must have this speed if the supernova is as far distant as claimed (about 170,000 light years). Astronomers found out to construct a model which should explain, how such enormous velocities are possible and they succeeded with the “light echo” concept. However, this concept is so unrealistic that I bring here in few lines the abstract of it: because the SN 1987A is to be seen almost exactly in the center of the above ring structure, the light echo model requires in this case sheets of dust lying in between the supernova and earth all exactly perpendicular to the line of sight, which render these rings. Otherwise, the supernova would not be seen in the center of the rings. But why should these hypothetical rings do us this favor? Did they correspond with each other and adjusted their position in such a uniform way so that big sizer astronomers are satisfied?
In my small universe these superluminal velocities are not needed, but we have ther simply a quite normal star. Another fact is that these ring structures are still so stable and retain their circular structure, although big size astronomers claim that they originated many thousands of years ago, expanding into space of many cubic miles, slowed down in velocity by interstellar material. If that would be a real picture the almost perfect ring structure would long ago have disappeared!
Further, there is much space in understanding these rings among big size astronomers: some rings are claimed to be real around the supernova, others which are difficult to explain (see above under “light echoes”) are claimed to be optical artifacts (light echoes). However, both types of rings have almost the same spectrum. If the light echo hypothesis is correct, the dust sheets hanging perpendicular to the line of sight would change the spectrum of the supernova to an absorption spectrum, introduced by these sheets and the material composing them. Nothing is to be seen of that.
Still more, the light intensity of the rings farther out is brighter or as bright as that of the inner rings. That “fact” cannot be explained by Gerardus' model. However, the small size plasma model, explaining the supernova as perhaps an electric discharge phenomenon of the outer, higher-charged layers (from differential rotation of highly ionized and hot gas of the supernova) has no problem with the above inconsistency. In that small size model the whole structure and development of ”supernovae” and rings is a compound system of electromagnetic phenomena, which are not dictated by distance but a model of electric currents in highly ionized gas and magnetic fields, which hold the system together and stationary (i.e., somewhat comparable with Gerardus' ”magnetic bottling parameters,” see page 28 in issue 73).
There is still another superluminal phenomenon, namely that connected
with the quasar 3C273 from which a jet is expelled at 25 times the
speed of light, as seen from different photographic plates taken since
1978. Naturally, this superluminal velocity is not accepted by
astronomers and converted to such models as light echoes to bring the
speed under that of light. However, this quasar shows still another
problem with this explanation, namely: the quasar itself is expanding
with about 30 times the speed of light. Now for the quasar itself, the light
echoes model cannot be used to explain these enormous velocities. And
now still another problem is there: the superluminal velocities between
the above jet and the quasar expansion itself differ, for the jet expands 25
times “c” while the quasar expands at 30 times “c.”
So I think the easiest way to explain these problems is that :
1)There are no light-travel times involved
2)The objects are much closer to us.
3)The formation of the jet and the expanding quasar might happen by fast electrons and highly ionized plasma. So the expansion velocity might be much smaller than the velocity of light. It could be only a few kilometers per second. That would mean that the quasar might be at least 100,000 times closer to us.
Cepheid variables
Now to the second issue, Cepheid stars, Gerardus' distance measures. Cepheid stars are claimed to be pulsating stars. At the beginning of this century, astronomers developed a model, which connected these claimed pulsations with a period-luminosity law and “calibrated” it to “known” big distances (or distance indicators). That is naturally circular reasoning to rely on such a measure, but there is still more inconsistent in this Cepheid model.
The “pulsation” periods repeat at such incredibly precise time intervals that it is hard to understand how a pulsating star, which, by the way, loses mass at each “pulsation,” can reproduce these high-precision cycles in time (”like a Swiss watch”). But we know high-precision cycles in astronomy: orbits of binary stars! And now it is very interesting that there are Cepheids (or other of these “pulsating” stars) which are simultaneously binary stars, the periods of which are exactly the same as the ”pulsation” period! So the question is: might it be that the “pulsation” theory is wrong, and the binary concept correct? And there are still more problems involved in the “pulsation” theory: the masses necessary for such a pulsating star are simply not there (in the big size universe concept), and still worse: a pulsating star would be brighter and hotter when contracting, and cooler and fainter when expanding. Actually, the converse is true.
And now comes the crucial point: if Cepheid stars are one of the pillars of the big size universe supporters, what about this main tool to measure these big sizes in the universe? The pulsating Cepheid stars are, as mentioned above, “calibrated” against other distance indicators. If the Cepheid indicators are based on a wrong physical model, then also the luminosity and mass considerations are wrong, and so are the distances!
Thus far on this matter. It could be enlarged on and on, because I see many further problems in this matter of the big size for the universe.
I sincerely hope that Gerardus prints these lines without his intervening comments in contrast to Biblical Astronomer no. 73. I hope that he has enough confidence, that his readers can judge the matter for themselves.
The mathematics of Einstein's theories and quantum physics is not tackled in this letter, though mentioned by Gerardus. But I have many facts (also the mathematics of them) in my files which make both theories, in my opinion, ridiculous.
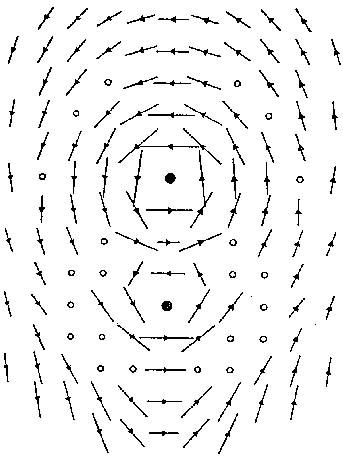
Figure 4: Outer rotation is much slower for gas than real (inner) rotation of both star companions (or even the rotation of the barycenter of both companions).